Analogové počítače jsou dnes jako dinosauři. Slepá, vyhynulá, zaniklá vývojová větev. Přitom nená tak dávno doba, kdy v šíři nasazení a přesnosti výpočtu analogové počítače drtily počítače digitální, takové, jaké známe dnes.

Analogové počítače, různě velké a různě vybavené, se samozřejmě vyráběly i v Československu. Proti digitálním jsou totiž jednodušší. Ovládat je ale vyžaduje znalost jejich fungování. Možná proto je známe jako obrovské a složitě vyhlížející krabice.
Kdyby nebyly integrované obvody a mikroprocesory, nebyly by digitální počítače jednoduché. Pravda, ZX-81 sestává ze zhruba čtyř čipů, a SoC řešení představují vlastně kompletní počítač, ale nebýt toho, jak velký by asi byl nejmenší digitální počítač?
Odpověď nám dá svou velikostí třeba Kenbak 1 (bez mikroprocesoru) nebo první verze PDP-8 (bez integrovaných obvodů) či dokonce Simon (reléový počítač).
(Minivac 601 s šesti relé nelze považovat za kompletní počítač.)
Jak malý by ale byl jednoduchý analogový počítač?

Odpověď nám dá malá stavebnice z roku 1960 – The Edmund Analog Computer Kit od společnosti Edmund Scientific Co. (Barrington, New Jersey).

Co na jeho stavbu potřebujeme?
Dva potenciometry 50 ohm, jeden potenciometr 1000 ohm, k potenciometrům průhledné plastové ukazatele. Pak měřák, kterému američani říkají „Meter 1-0-1 ma.“ (miliampérmetr), spínací tlačítko, držák na baterii (pokud se bude počítač napájet z baterie), izolovaný drát, panel, na který se budou kreslit stupnice (originální kit je měl předtištěné) a krabice (v originále 20×8,5×2 palce, přiměřeně velikosti součástek a stupnic na panelu si ji lze ale vyrobit i mnohem menší).

Na průhledné ukazatele, které se připevní ke knofíkům potenciometrů, se provede nitkovitá ryska.
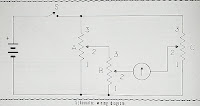
Součástky se zapojí podle obrázků (nezapomeňte, že nákres zapojení je zobrazen zezadu, tedy zrcadlově obráceně oproti čelnímu panelu).

Celá sranda s třemi poťáky a jedním měřákem je opravdu kompletní analogový počítač, na kterém se dají počítat i poměrně složité věci, jak uvidíte. Zjistíme, že na třech potenciometrech jde řešit i balistické tabulky – tedy něco, co ve světě digitálních počítačů vyžadovalo potvoru velikosti ENIACu.
Manuál uvádí přesnost kitu s chybou kolem 2-3%, což je údajně dostatečné (podle manuálu se přesnost běžných analogových počítačů pohybuje kolem 1% chyby, zatímco pro většinu inženýrských výpočtů je dostatečná i 5% chyba a proto přesnost i tak malého kitu, jakým je Edmund, bohatě převyšující požadavky většiny aplikací).

Násobení

Základní rovnice pro násobení na Edmundu je AxB=C (písmena A, B, C označují jednotlivé potenciometry, viz obrázky zapojení).

Pro vynásobení dvou čísel se jeden činitel nastaví na potenciometru A, druhý na potenciometru B.. Pak se stiskne a podrží tlačítko (v originále zvané „test button“), během toho se otáčí potenciometrem C tak, aby se měřák dostal na nulu (ověřit si, že je opravdu na nule, můžete i tak, že při puštění tlačítka se už ukazatel nepohne).
Výýsledek se odečte na stupnici potenciometru C (originální kit má několik stupnic – lineární, logaritmickou, sinus a tangens plus při číslování i z druhé strany i cosinus a cotangens – při násobení se používá lineární stupnice).
Na lineární stupnici je dvojí dělení – na setiny a na desetiny.
Takže, chceme třeba vynásobit 0,4 x 0,8.
Na jednom poťáku nastavíme 0,4, na druhém 0.8. Po nastavení nuly potenciometrem C by měl ukazovat mezi 0,31 a 0,33.

Dělení

Základní rovnice násobení (AxB=C) se dá přepsat na A=C/B.
Tedy pro vydělení čísel nastavíme dělence na poťáku C, dělitele na poťáku B a pak zkoušíme nastavit na měříku nulu pomocí potenciometru A.
Výsledné číslo ukazuje stupnice potenciometru A.
Například pro výpočet 0,48 / 0,6 nastavíme 0,48 na C a 0,6 na B. Po nastavení nuly na měřáku by poťák A měl ukazovat mezi 0,785 a 0,815 (tento interval představuje prý dostatečnou přesnost).
Ještě je tu jedna věc – zkuste si vydělit  0,82 / 0,61.
Pokud nastavíte 0,82 na C a 0,61 na B, nepodaří se vám dosáhnout nuly, protože výsledek je větší než 1. Rovnici je proto třeba chápat jako (0,83 / 0,61) x 10, tedy zmenšit dělence o řád.
Nastavte tedy poťák C ne na .82, ale na 0,082 (tak přesně, jak na stupnici dokážete). Výsledek má být 0,136 x 10 (to je ten náš ztracený řád), tedy 1,36. Za spolehlivý výsledek můžete považovat dosažení intervalu 0,125 až 0,145, což je ovlivněno tím, že jedno z čísel bylo menší než 0,1 (což zvyšuje chybu).

Jak to pracuje?

Potenciometr A snižuje napětí podle svého nastavení (s jezdcem v polovině sníží napětí na polovinu, ve čtvrtině na čtvrtinu, tak jak to odpovídá lineární stupnici).
Potenciometr B je zapojen jedním vývodem na jezdec potenciometru A, tím se výstupní napětí z potenciometru A násobí hodnotou nastavenou potenciometrem B (což odpovídá uspořádáním pro uvedené rovnice násobení a dělení).
Výstupní napětí by se dalo měřiit voltmetrem (a rovnou by dávalo výsledky), malé rozdíly v napětí jsou ale špatně detekovatelné. Proto je použit ampérmetr v rozsahu 1 ma s dalším potenciometrem, Miliampérmetr se ustálí na nule (proud neprochází), když je napětí na potenciometru B stejné jako na potenciometru C.
To umožňuje detekovat změny v řádech milivoltů.

Přesnost

Protože se chyby sčítají, pak by při použití potenciometrů se standardní toolerancí 10% narůstala chyba na 30%. V originálním kitu jsou proto použity dražší potenciometry s výslednou chybou 3%.
K dalšímu snížení chyby přispějí rozdíly v rozsahu potenciometrů. Pokud by potenciometr B měl 10x větší odpor než potenciometr A, bude chyba 2%. Při 20x větším odporu (jako je to v Edmundu) bude chyba do 1%.
Chyba je větší při nastavení nízkých hodnot. Například pro A=0,1 a B=0,3 je výstup potenciometru B (ze zdroje 3V) 3×0,1×0,3, tedy 0.09 V, 90 milivoltů.
Pokud měřák zvládne nulu vtěsnat do intervalu 2 mV, bude chyba kolem 2%. Pokud se ale nastaví A=0.5 a B=0,9, pak na výstupu B bude napětí 3×0.5×0.9, což je 1,35V a chyba se bude blížit nule.

Stupnice

Už jsem nadhodil, že je u potenciometrů několik stupnic.
O lineární (v rozsahu 0 .. 1,0) už víme.
Pak je tu sinus (0 .. 90 stupňů) a cosinus (90 .. 0 stupňů).
Tangens (0 .. 45 stupňů) a cotangens (45 .. 0 stupňů).
A logaritmická stupnice (1 .. 10).
Protože sinus a cosinus jsou komplementární, jsou v originále na stejné stupnici (jen je z jedné strany číslována vzestupně a z druhé strany sestupně). Podobně to platí pro tangens a cotangens.
To, že lze provádět výpočty i mimo číselný rozsah stupnic pomocí mocnin deseti je asi jasné a nemá smysl podrobněji opisovat z manuálu příslušnou kapitolu, která to vysvětluje.
Ale na ukázku – chtějme vynásobit 378000 x 0,000012. tedy 378E3 x 12E-6. Vynásobením 378×12 (respektive na lineární stupnici 0.378x 0.12, plus příslušný posun v řádech) získáme 4536 (tedy ona nám to nepřesnost Edmunda nedovolí, ukáže nám přinejlepším něco mezi 0.450 a 0.455). Z hlavy už můžeme sečíst exponenty, a protože 3+(-6) = -3, posuneme čárku desetinnou o tři místa na 4,536.
Možná to vypadá zmateně, ale ve své době to bylo naprosto normální, protože úplně stejně se uvažovalo při počítání na stupnici logaritmického pravítka (které se od stupnic použitých na Edmundu vlastně neliší). A logáro tehdy musel ovládat opravdu každý, kdo chtěl trochu víc počítat.
V zásadě se dá říct, vzhledem k jednoduchosti zapojení, že je Edmund takovým elektronickým logaritmickým pravítkem s různými stupnicemi (složitější analogové počítače se pak už ale logáru svými možnostmi značně vzdalují).

Po zacvičení to v praxi jde celkem jednoduše:
37 x 0,092
Nastavíme si 0,37 a 0,92 (jako 0,37E2 x 0,92E-1). Po nastavení nuly na měřáku je výsledek hodnota ukazovaná potenciometrem C krát 10.
0,000885 x 0,00000567
Nastavíme si 0,855 (E-3) a 0,567 (E-5). Protože (-3)+(-5) je -8, je nutno výsledek na potenciometru C vynásobit (10 na -8).

A dělení:
480/6
Nastavíme 0,48 a 0,6. Všimněte si, že hodnoty jsou stejné, jako v příkladu, který je uveden u popisu dělení. Jen v tomto případě je nutno výsledek na potenciometru A vynásobit (10 na 2), výsledek je tedy 80.
0,083/0,610
Nastavíme-li dělení na 0,83/0,61 (respektive 0,83E-1 x 0,61E3), nejde pomocí potenciometru A nastavit nula (víme proč – i v tomto případě jsou totiž hodnoty na potenciometrech stejné, jako v příkladu u popisu dělení; výsledek je totiž větší než 1 a tedy mimo rozsah stupnice potenciometru).
Potřebujeme tedy dělence zmenšit o řád. Spočítáme tedy 0.083/0,61 s příslušnými řádovými přenosy (0,83 x 0,61E3), výsledek se násobí (10 na 3), tedy dělí (10 na -3).

Mocniny a odmocniny

Edmund samozřejmě umí mocnit.
Protože mocnina dvou je vynásobení čísla sama sebou, nastaví se mocněné číslo na potenciometrech A a B a výsledek se (po nulování) odečte na potenciometru C.

0,4 na druhou – nastavíme 0,4 a 0,4, odečteme výsledek 0.16.
40 na druhou – nastavení je stejné, jen je potřeba chápat ho jako 0,4E2 na druhou, což je 0,4 na druhou krát (10 na druhou) na druhou, což je 10 na čtvrtou. 0,16E4 je 1600.

Pro vypočtení druhé odmocniny je třeba rozdělit číslo na mantisu v rozsahu 0,1 až 1,0 a desítkový exponent (mocninu deseti).

Pokud je mocnina exponentu sudá (E2, E4, E-6), nastaví se základ čísla na potenciometru C a pak se snažíme na měřáku dosáhnout nulu nastavením stejné hodnoty na potenciometru A a B.
Odmocnicna z 3200 například – je to 0,32E4. Na poťáku C nastavíme 0,32.
A a B můžeme oba nastavit na 1, stisknout tlačítko testu a otáčet současně stejnou rychlostí oběma potenciometry k nižším hodnotám. Pokud dosáhnete na obou nuly současně, otáčeli jste jimi opravdu spřaženě, takže stejným způsobem otáčíte zase nahoru do místa, kde se měřák ustálí na nule, mělo by to být u 0,566. (Pokud při sestupném otáčení nedorazí potenciometry k nule současně, neotáčíte jimi dost spřaženě – vraťte je na jedničku a vyzkoušejte jiný způsob otáčení.)
Odmocnina z 10 na 4 je 10 na 2 (pro odmocnění mocniny deseti stačí exponent vydělit dvěma), takže 0,556E2 je 56,6.

Pokud je mocnina exponentu lichá (E3, E-5), jsou dvě možnosti:
Postupovat stejně jako u sudých exponentů – nastavit odmocňovanou mantisu na poťáku C, kroutit A a B současně do nastavení nuly na měřáku.
Výsledek na potenciometru A ponecháme a na poťáku B nastavíme odmocninu z 0,1 (což je přibližně 0,316). Pak znovu na měřáku nastavíme nulu pomocí potenciometru C.
Například odmocnina z 320 (0,32E3): Nastavíme 0,32, odmocníme, máme výsledek 0,566, ten ponecháme na A, na B nastavíme 0,316 a kroutíme C, které se zastaví na 0,179. Vynásobíme stem a máme výsledek.
SQR 320 = SQR (0,32)xSQR (10 na 3) = SQR (0,32) x SQR (10 na -1) x SQR (10 na 4) = SQR (0,32) x SQR (0,316) x SQR (10 na 2)

Druhá metoda je rozdělit 320 na 0,032E4. Na potenciometru C pak nastavit 0,032 a s tím pak odmocňovat – samozřejmě, jak víme, použitím tak malého čísla se snižuje přesnost.

Sinus a cosinus

Sinus a kosinus odpovídajícího čísla na lineární stupnici jsou uvedeny na sinusové (a kosinusové) stupnici. Pokud tedy nastavím na sinusové stupnici 30 stupňů, na lineární hned vidím, že je to 0,5. A s tím se vstupuje do výpočtů.
0,41 x cos 56
Na poťáku A nastavíme 0,41 a na kosinové stupnici poťáku B nastavíme 56. Na lineární stupnici poťáku C máme po nastavení měřáku na nulu výsledek.
78 / sin 62
Nastavíme na C 0.78, na sinusové stupnici poťáku B nastavíme 62 a nulujeme měřák pomocí A, které ukazuje výsledek (0,884, musíme vynásobit stem a získat 88,4) na lineární stupnici.
86 / sin 23
Protože 0,86 / sin 23 je větší než 1, musíme na C nastavit 0,86, na sinusové stupnici B nastavit 23 a po vynulování pomocí A nám jeho lineární stupnice ukazuje 0.22, a protože jsme dělili tisícem, musíme i násobit tisícem a výsledek je 220.

Tangens a cotangens

Tangens stupnice je pro úhly od 0 do 45 stupňů a cotangens od 45 stupňů.
Vztah je přitom takový, že násobení tangentem odpovídá dělení cotangentem (převrácená hodnota).
61 x tan 38
Na lineární stupnici A se nastaví 0.61, na tangentové stupnici B se nastaví 38, pomocí C se nuluje a ukazuje výsledek 0,476 (po doplnění řádů 47,6).
81 x cot 69
Na lineární stupnici A se nastaví 0,81, na cotangentové stupnici B 69, pomocí C se vynuluje a ukazuje výsledek 0,311 (po doplnění řádů 31,1),
31 x tan 56
Protože jde o úhel větší než 45 stupňů, převedeme na 31 / tan 56.
Takže na lineární stupnici C nastavíme 0,31, na kotangentové stupnici B 56, nulujeme po’tákem A a ukazuje výsledek 0,46 (po doplnění řádů 46).
Podobně pro násobení kotangentem úhlu pod 45 stupňů převedeme na dělení tangentem.

Logaritmy

Je potřeba upozornit, že Edmund je jen jednoduché zařízení s víceméně lineární charakteristikou potenciometrů, které jsou jen doplněné i o logaritmické stupnice – z toho vyplývá i určité omezení přesnosti výpočtu. „Velké“ analogové počítače pro výpočty logaritmů používají zapojení s opravdu logaritmickými charakteristikami.
Přesto se dá na Edmundu s logaritmy pracovat minimálně na úrovni logaritmického pravítka.
Základním vztahem je, že (X na A) = Y odpovídá A x log X = log Y.

5 na druhou
Pokud chceme toto spočítat pomocí logaritmu a ne násobení, postupujme takto:
Nastavíme lineární stupnici A 0,2, na logaritmické stupnici B 5. Nulujeme na potenciometru C a mezivýsledek odečítáme na jeho lineární stupnici 0,14 (po doplnění řádů 1,4). Tím jsme získali log Y. Nyní C nastavíme na desetinnou část (0,4) na lineární stupnici  a na logaritmické stupnici odečteme 2,5. Jednička v celočíselné části mezivýslednu znamená, že máme násobit deseti, výsledek je tedy 25 (pokud je celočíselná část nula, nemusí se nic násobit, protože by se násobilo jedničkou; pro 1 násobíme 10, pro 2 násobíme 100, pro 3 násobíme 1000, protože 1 je log 10, 2 je log 100, 3 je log 1000).

Zkusme něco složitějšího:
7 na třetí
Na lineární stupnici A nastavte 0,3, na logaritmické stupnici B nastavte 0,7. Po nulování pomocí C odečítáme (na lineární stupnici) mezivýsledek 0,254, po doplnění řádů 2,54. Na lineární stupnici C nastavíme 0,54 (desetinná část mezivýsledku), na logaritmické stupnici odečteme 3,45. Násobíme stem a máme výsledek 345 (zcela přesný výsledek, tedy 7x7x7, by byl 343; všimněte si, že pokud byste mezivýsledek odečetli jako 0,25, byl by výsledek 315, pokud jako 0,26, byl by výsledek 400).

9 na 4,3
Toto už pomocí násobení nespočítáte. Nastavte tedy 0,43 na lineární stupnici A, na logaritmické stupnici B 9, nulujet pomocí C a ukazuje mezivýsledek 0,41, po přenosu řádů 4,1. Nastavíme na lineární stupnici C 0,1. Na logaritmické stupnici C čteme 1,26. Krát 1E4 je 12 600 (skutečný výsledek je blíž k 12700, ale pokud bylo dosaženo intervalu 12 500 .. 12 900, je chyba menší než 2%.

čtvrtá odmocnina z 9
Výraz lze zapsat i jako 9 na jednu čtvrtinu, tedy 9 na 0,25. Nastavte na lineární stupnici A 0.25, 9 na logaritmické stupnici B, po vynulování C dává na logaritmické stupnici 1,73 (protože není potřeba přenos řádů, dá se hodnota odečíst přímo).

Vypadá to, že toho není moc, co Edmund umí.
Proto si ještě ukážeme, co všechno se dá pomocí jeho omezených schopností řešit. Zjistíme, že na třech potenciometrech jde řešit i balistické tabulky – tedy něco, co ve světě digitálních počítačů vyžadovalo potvoru velikosti ENIACu.